How to: testresultaten op de juiste manier interpreteren

Het beoordelen van je testresultaten blijft een lastige klus. Natuurlijk willen we het liefst zoveel mogelijk positieve resultaten aan onze klant, baas of collega’s laten zien, maar het moet niet ten koste gaan van de betrouwbaarheid. Om maar te zwijgen over de angst voor een vals-positief resultaat, waarbij je een aanpassing laat doorvoeren die zelfs voor een verslechtering van de resultaten zorgt.

We zien te vaak situaties langskomen waarbij een resultaat wordt afgeschoten terwijl de kans dat dat resultaat voor verbetering zorgt eigenlijk juist het grootst is. Het heeft allemaal te maken met hoe de resultaten geïnterpreteerd worden. In veel gevallen wordt een uitslag gebruikt om een ‘ja’ of een ‘nee’ antwoord te geven op de vraag of een aanpassing op de website geïmplementeerd moet worden. Terwijl een resultaat eigenlijk gezien moet worden als een analyse van het risico dat hangt aan het wel of niet doorvoeren van een aanpassing.

Twee manieren voor het interpreteren van testresultaten

Grofweg zijn er twee manieren om een testresultaat te beoordelen. Je kunt dit doen via de Frequentist-methode of via de Bayesian-methode.

Frequentist

Als je je resultaten beoordeelt met de Frequentist-methode, test je of een gebeurtenis optreedt of niet. Het berekent de kans op herhaling van die gebeurtenis op de lange termijn. In het geval van een A/B test is jouw hypothese de gebeurtenis die je test. Als je hypothese niet optreedt (dat wil zeggen niet voor verbetering zorgt) dan krijg je een ‘nee’ als resultaat. Als hij wel optreedt dan is het resultaat een ‘ja’. Er zijn dus maar twee uitkomsten mogelijk.

Bayesian

De Bayesian-methode werkt uiteraard anders. Er is geen ‘ja’ of ‘nee’ uitkomst. In plaats daarvan werkt Bayesian met waarschijnlijkheden. Het berekent de kans dat jouw hypothese succesvol is op een schaal van 1% tot 100%. Hoe groter de kans, hoe zekerder je van je zaak kunt zijn, maar je bepaalt zelf vanaf wanneer je een aanname acceptabel vindt. Daarbij houd je ook rekening met andere factoren, zoals kosten en baten.

Worst case vs. best case

Ik ben van mening dat de Bayesian-methode een meer correcte manier is om een resultaat op zijn waarde te schatten. Er is namelijk een beter verwachtingsmanagement. Je bent niet alleen bezig met de gemiddelde percentages, maar je kijkt ook naar wat er gebeurt als deze gemiddelden af blijken te wijken.

Daarbij is het eindresultaat een risicoanalyse waarin we kijken naar alle mogelijke effecten die het doorvoeren van een resultaat kan hebben. Wat gebeurt er in het beste geval? Maar ook, wat is het effect als we toch aan kortste eind trekken?

Welke data moet je gaan interpreteren?

Goed. Genoeg over de onderliggende methode. Terug naar dat waar het om gaat, namelijk het interpreteren van je resultaten. Voordat ik een aantal rapportages met je ga doornemen, wil ik graag nog even de statistieken met je doorlopen die in zo’n rapportage terugkomen.

Testdata

Dit zijn de data die je rechtstreeks uit je test kunt halen. Die bestaan uit:

• Het aantal variaties
• Het aantal bezoekers per variatie
• Het aantal conversies per variatie

Op basis van deze data worden de overige statistieken berekend.

Gemiddelde conversiepercentage

Het aantal conversies gedeeld door het aantal bezoekers geeft het gemiddelde conversiepercentage per variant weer.

Verbetering

Dit is het verschil tussen de gemiddelde conversiepercentages. Het kan een verbetering aangeven, maar in sommige gevallen ook een verslechtering. In dat geval wordt er een negatief percentage weergegeven.

Betrouwbaarheidsintervallen

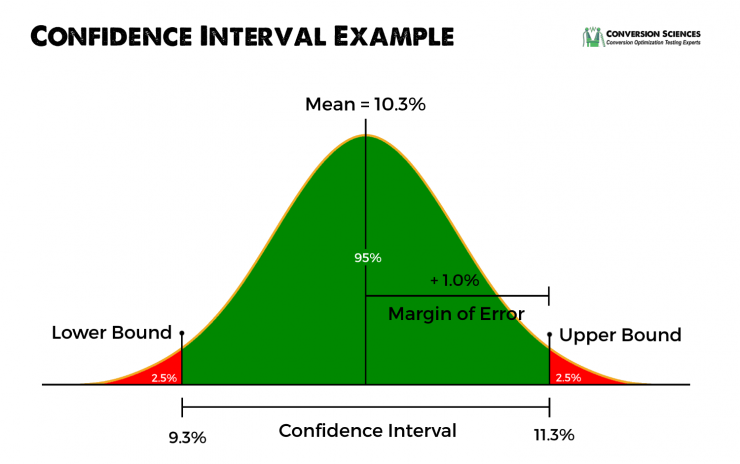
Elk gemiddeld percentage wordt voorzien van een betrouwbaarheidsinterval. Deze betrouwbaarheidsintervallen geven de onder- en de bovengrens van het gemiddelde percentage aan. Dit wordt ook wel de foutmarge genoemd. Het is een meting van de afwijking die het gemiddelde in de praktijk zou kunnen hebben.

In onze rapportage maken we gebruik van intervallen van 95%, wat betekent dat er een 95% kans is dat het daadwerkelijke conversiepercentage tussen de onder- en bovengrens gaat vallen.

Betrouwbaarheid

De betrouwbaarheid geeft de kans weer dat het origineel verslagen wordt door de variant. Hoe hoger dit percentage hoe kleiner het risico dat een resultaat op toevalligheden wordt gebaseerd. Betrouwbaarheid wordt dan ook weergegeven als in kans van 1% tot 100%.

Hoe beoordelen we deze testresultaten?

Grip hebben op de data en de statistieken is niet hetzelfde als een resultaat beoordelen. Want wat proberen de bovenstaande cijfers je nou te vertellen? Laten we daarom twee rapportages doornemen om te bespreken wat de data ons vertellen en hoe we daaraan conclusies kunnen verbinden.

Belangrijk om te onthouden tijdens het interpreteren van de data:

• Zoek niet direct naar een ‘ja’ of een ‘nee’, maar neem de tijd om de statistieken goed te bekijken voordat je direct een conclusie gaat trekken;
• Onthoud dat er ook niet altijd een duidelijke ‘ja’ of ‘nee’ uit te halen valt; zoals gezegd is de interpretatie van een resultaat een risicoanalyse waarbij meerdere factoren van invloed zijn die niet allemaal in de rapportage zijn terug te vinden (zoals bijvoorbeeld de kosten die gemoeid zullen zijn met het doorvoeren van de aanpassing uit de A/B test);
• Het verbeteringspercentage is belangrijker dan het gemiddelde conversiepercentage van A en B;
• Neem een resultaat pas in overweging als het betrouwbaarheidspercentage boven een voor jou acceptabele grens zit.

Hoe beoordelen we zo’n resultaat dan? Dat gebeurt in drie stappen. Eerst kijken we objectief naar wat we in eerste instantie zien in de aantallen, daar laten we een risicoanalyse op los en uiteindelijk komen we met een conclusie waarop we de keuze baseren om een aanpassing wel of niet door te voeren.

Het eerste voorbeeld (A is beter dan B)

Eerste conclusie

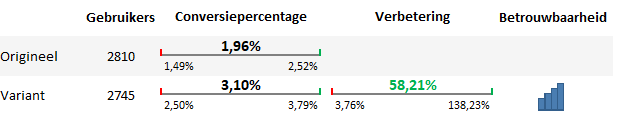
Op basis van de gemiddelde conversiepercentages per variant zou je kunnen concluderen dat we ruim 1% in conversie stijgen als we de variant implementeren (van 1,96% naar 3,10%).

Risicoanalyse

De betrouwbaarheidsintervallen laten zien dat het daadwerkelijke resultaat van het origineel ergens tussen de 1,49 – 2,52% zal zitten. Voor de variant is dit ergens tussen 2,5% en 3,79%. Er zit wel wat overlap tussen de twee bandbreedtes, dus in theorie is er een kans dat A en B gelijk aan elkaar zullen presteren.

Het verbeteringspercentage is louter positief. De kans is dus 95% dat de uiteindelijke verbetering tussen de 3,76% en de 138,23% ligt. Dat betekent dat we in het slechtste geval nog steeds een verbetering in de resultaten te pakken hebben, al is het in dat geval wel maar een bescheiden verbetering.

Eindconclusie

De variant presteert beter dan het origineel, waarschijnlijk nog een stuk beter ook. De kans dat de variant uiteindelijk toch nog slechter gaat presteren is heel erg klein, dus we hebben hier sowieso met een verbetering te maken. Dat geldt ook voor de kans dat de verbetering 0% is, en A en B dus aan elkaar gelijk zijn.

Natuurlijk blijft er wel een mogelijkheid over dat de uiteindelijke verbetering aan de lage kant is, dus als de aanpassing een grote investering vraagt is dit een afweging die gemaakt moet worden. Uiteindelijk is de kans op een hoger verbeteringspercentage nog steeds het grootst.

Een tweede voorbeeld (B is gelijk aan A)

Eerste conclusie

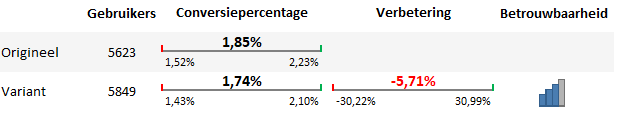
De conversiepercentages van A en B liggen dicht bij elkaar in de buurt. Het is dan ook logisch dat de onder- en bovengrens veel overlap met elkaar vertonen. Dat betekent dat er een grote kans is dat het minimale verschil berust op toeval en niet omdat er iets daadwerkelijk slechter presteert.

Risicoanalyse

Ondanks het feit dat de gemiddelde verbetering negatief is, laat het betrouwbaarheidsinterval zien dat er eigenlijk geen verschil is tussen de beide varianten. Het verschil komt nagenoeg in het midden uit, wat waarschijnlijk zal betekenen dat we uiteindelijk geen verschil zullen constateren

Eindconclusie

De nieuwe variant presteert op het oog slechter dan het origineel, de bandbreedte laat zien dat het verschil eigenlijk zo minimaal dat er geen echt verschil is te meten. Het verschil is ontstaan door toeval en er hoeft dan ook geen verdere actie te worden ondernomen. Doorvoeren is niet te adviseren.

Het laatste voorbeeld (A is beter dan B)

Eerste conclusie

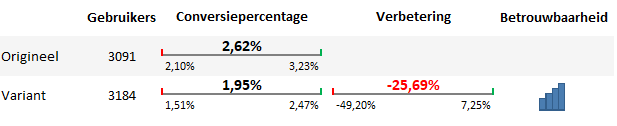
De gemiddelde conversiepercentages liggen ver uit elkaar, maar de onder- en bovengrens laten wel overlap zien.

Risicoanalyse

De verbetering is echter negatief. Er is maar een hele kleine kans dat de verbetering uiteindelijk boven de 7,25% uitkomt. Er is dus wel een kans op een positief resultaat (zoals ook te zien in de overlap tussen de twee conversiepercentages), maar die kans is wel heel klein. Het doorvoeren van de aanpassingen zou dus een groot risico met zich meebrengen.

Eindconclusie

De nieuwe variant presteert slechter dan het origineel. De betrouwbaarheid is groot; dat betekent vrijwel zeker dat het verschil tussen de varianten klopt. In dit geval zal het doorvoeren van de aanpassingen dan ook leiden tot een conversiedaling en daarom niet aan te raden.

Ten slotte nog dit

Ik hoop dat ik je wat meer inzicht heb kunnen geven in het interpreteren van testresultaten. De inschatting van het risico dat een eventuele implementatie met zich meebrengt, is het belangrijkste onderdeel. De statistieken geven daarvoor het houvast:

• De betrouwbaarheid stelt ons in staat om vast te stellen of een test in een positieve of negatieve richting wijst. Het resultaat kan statistisch gezien significant zijn, maar in de praktijk geen winst opleveren, bijvoorbeeld omdat de implementatiekosten te hoog zijn. Het is dus belangrijk om verder te kijken dan de betrouwbaarheid alleen;
• Het gemiddelde conversiepercentage geeft een redelijke indicatie van de prestaties van de varianten. De betrouwbaarheidsintervallen geven een indicatie van de afwijkingen die daarop kunnen voorkomen. Als er geen of weinig overlap tussen de twee betrouwbaarheidsintervallen is, dan is de onzekerheid kleiner;
• Het betrouwbaarheidsinterval voor de verbetering geeft een indicatie van het resultaat dat we kunnen verwachten als we A vervangen door B. Dit is dus een belangrijke statistiek om in de eindconclusie in overweging te nemen.

Handige bronnen

• https://support.abtasty.com/hc/en-us/articles/205811297
• https://www.abtasty.com/blog/clever-stats-finally-statistics-suited-to-your-needs/
• https://betterexplained.com/articles/an-intuitive-and-short-explanation-of-bayes-theorem/
• https://blog.kissmetrics.com/how-ab-testing-works/
• https://conversionsciences.com/blog/ab-testing-statistics/